Introduction

As humans, we continually seek patterns. They fascinate me and as a child I would stare at clouds, conjuring creatures; attempting to make sense of the abstract swirls above. Shermer (2008), argues that through evolution, our brains have become "pattern recognising machines", and no matter where we look, we try to make sense of the world around us. Constantly searching for patterns makes sense from an evolutionary point of view. Seeing a pattern that is not there is preferable to missing one that is, as it could be a matter of life and death (Robson, 2014). Whilst we have not yet evolved to recognise the difference between real and false patterns, the trait of being vigilant and always thinking about patterns has become a subconscious action (Shermer, 2008).

In this article I will consider the relationship between fractal patterns and the unconscious mind. I will explain fractals, the subconscious and why we are drawn to them. I will explore where fractals are found, where they are embedded in popular culture and how they affect our lives. By understanding fractal patterns, I will explore if they are reflected in the unconscious mind. To do this, I will consider the brain's response to fractals and whether this influences people's responses. Finally. I wonder whether my brain is the most significant influence of all.

Nature's Hidden Treasures

Nature has mesmerised humans since the beginning of time; colours, shapes and textures combining to create wondrous scenery. Nature often disguises itself as something without order and regularity; clouds forming different shapes, and trees growing spindly branches and twigs. However, the opposite is true, as nature is made from simple formulae which create infinite complexities. Remarkably, patterns follow mathematical and physical principles; ripples in windblown sand mimic a zebra's markings and a tree's branches imitate a river network. Whist these structures appear to be unpredictable, there is a hidden pattern, a logic, one only apparent when looked at mathematically (Ball, 2016).

The similarities between broccoli, a snowflake and blood vessels are not immediately obvious; however, they are all fractals. A fractal is defined as "a structure or object whose shape repeats at ever finer scales" (Ball, 2016, p282). Fractals are found throughout Nature's design; hidden in plain sight within plants, weather systems, and even in our bodies. Within the margins of a snowflake, can be seen what scientists describe as the "fingerprint of Nature" (Fractals and Jackson Pollock, 2011).

On closer inspection, a snowflake is made up of smaller, connecting snowflakes, and zooming in will show how these snowflakes are made up of even smaller snowflakes and so on until infinity (Keating, 2020). As the magnification of a snowflake increases, shapes within it repeat themselves on a smaller scale [fig. 1]. This creates the natural pattern we know as fractals (Fractals and Jackson Pollock, 2011). This fractal pattern is mirrored in our bodies as our lungs, kidneys, and the rhythm of our beating heart demonstrate the jagged, repeated pattern of a fractal (Hunting the Hidden Dimension, 2008).

Figure 1: The 'Koch Snowflake curve' designed by Swedish mathematician Helge Von Kock, 1904

For centuries, observations have been made about shapes found in Nature, and humans have tried to make sense of what they see. Leonardo da Vinci stated, "All the branches of a tree at every stage of its height when put together are equal in thickness to the trunk" (Da Vinci, 2012, p206). Although the science of the fractal code was yet undiscovered, humans were always making sense of such patterns.

Noticing that patterns were often found in Nature, Benoît Mandelbrot, a mathematician began to research the phenomenon. His investigations led to his discovery of fractals in 1975 (Moore, n.d.). Mandelbrot explained them as "geometric shapes that when divided into parts, each part would be a smaller replica of the whole shape" (Moore, n.d.). He took the Latin word 'fractus' meaning broken or fractured and used the term 'fractal' as the new scientific term for the mathematical expression explaining the replication of shapes.

Examples of fractals include trees, clouds and rocks because they display the same qualities and follow the same rules; giant clouds and rocks are identical to tiny ones. "You can't tell if you're looking at an enormous mountain or a humble boulder" (The Code, 2011). Trees demonstrate the incredible power of fractal systems; their great complexity stemming from very simple rules. Grow and divide, grow and divide, repeat. A single branch looks like the rest of the tree and twigs coming from the branch hold the same shape. Thus, the same pattern appears again and again but at a smaller scale. This growing structure is found throughout nature (The Code, 2011).

Behind this infinite algorithm is a mathematical structure. Mandelbrot explored how patterns in nature could be explained through mathematics. He created the 'Mandelbrot set'; an arrangement of circles and swirls echoing themselves at smaller and smaller scales infinitely (fig. 2). This endless complexity came from one very simple mathematical function (Hunting the Hidden Dimension, 2008).

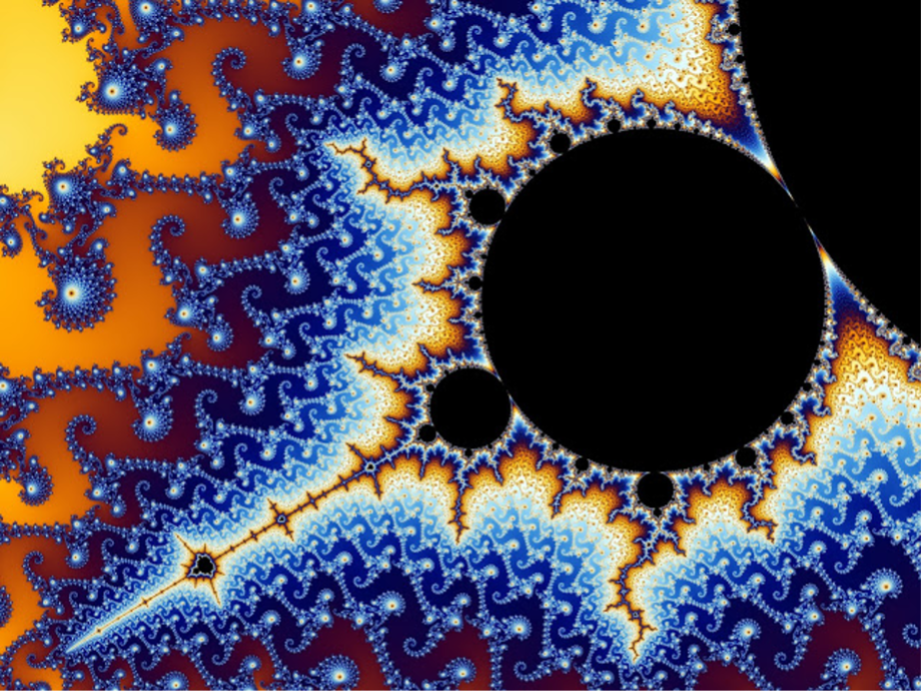Figure 2: The Mandelbrot set for the process F(z) = z2 + c, Benoit Mandelbrot, 1983

Being able to share his theory didn't just allow Mandelbrot to explain the growth of trees. He could describe seemingly random shapes through similar, simple mathematical codes (Mandelbrot, 1983). "When it was explained, people could see forms which had previously gone unnoticed. He made the invisible visible and found order within disorder" (Hunting the Hidden Dimension, 2008). Being immersed in a fractal-rich environment allows us to process them extremely quickly, even if we are unaware of doing so (Cepelewicz, 2017).

Next, I will consider the idea of the conscious and subconscious mind. and aim to find whether fractals could be embedded in the subconscious.

The Beautiful Brain

In this section, I will consider the role of the subconscious in our attraction to fractals by considering a case study which looks objectively at the brain's response to stimuli. Although most people are unaware that this pattern has a specific name, our brains have been subconsciously taking in fractals every day (Shermer, 2008). The idea of consciousness is infamously obscure and difficult to analyse as it is unclear what the term 'subconscious' means (Next Observer, 2019). Consciousness is non-physical; it is the part of us that is hard to understand; however new research and analysis using brain scans may be able to shed some light on the subject of our subconscious being captivated with patterns and fractals (Observer, 2020). Freud uses the subconscious to explain "associations and impulses that are not accessible to the consciousness" (Freud, 2001, p57). The dictionary defines the subconscious as "of or concerning the part of the mind of which one is not fully aware, but which influences one's actions and feelings." (Subconscious | Definition of Subconscious by Oxford Dictionary on Lexico.com also meaning of Subconscious, 2021).

A case study of Jason Padgett gives great insight into the visual processing of subconscious patterns. Padgett had never taken an interest in maths. He described maths as 'stupid', questioning how it was used in the real world (Padgett, 2020). Padgett was attacked in September 2002 (Incredible Medicine: Dr Weston's Casebook, 2020). He had no memory of the attack beyond a blow to his head but was left with severe concussion, post-traumatic stress disorder (PTSD), obsessive compulsive disorder (OCD) and a new way of seeing the world (Keating, 2020).

As a result of his injuries, Padgett began to notice patterns in everyday tasks and objects; brushing his teeth had a mathematical element to it (Keating, 2020). He reported that water gushing down the drain no longer flowed smoothly, but looked like it was made up from numerous, tangent lines (Padgett, 2020). He noticed patterns everywhere he looked, including in trees, clouds and water and was able to draw complicated geometric fractal patterns by hand.

He stumbled across a website about fractals which struck a chord and he felt able to use a new language of mathematical patterns (Keating, 2020). He viewed the world as a series of complex geometrical shapes and despite an increasing fascination with fractal shapes, was unable to understand or explain them (Incredible Medicine: Dr Weston's Casebook, 2020). Describing how the television worked to his daughter, brought clarity to Padgett's confusion.

When looking at the screen, Padgett's daughter could only see a circle, but he helped her notice a series of squares and rectangles, which on closer inspection, became zigzags. This reminded Padgett of his observations following his accident, when everything curved appeared to be slightly pixelated (Padgett, 2020). He explored this obsessively through drawing (fig. 3), and believed his sketches "held the key to the universe" (Keating, 2020).

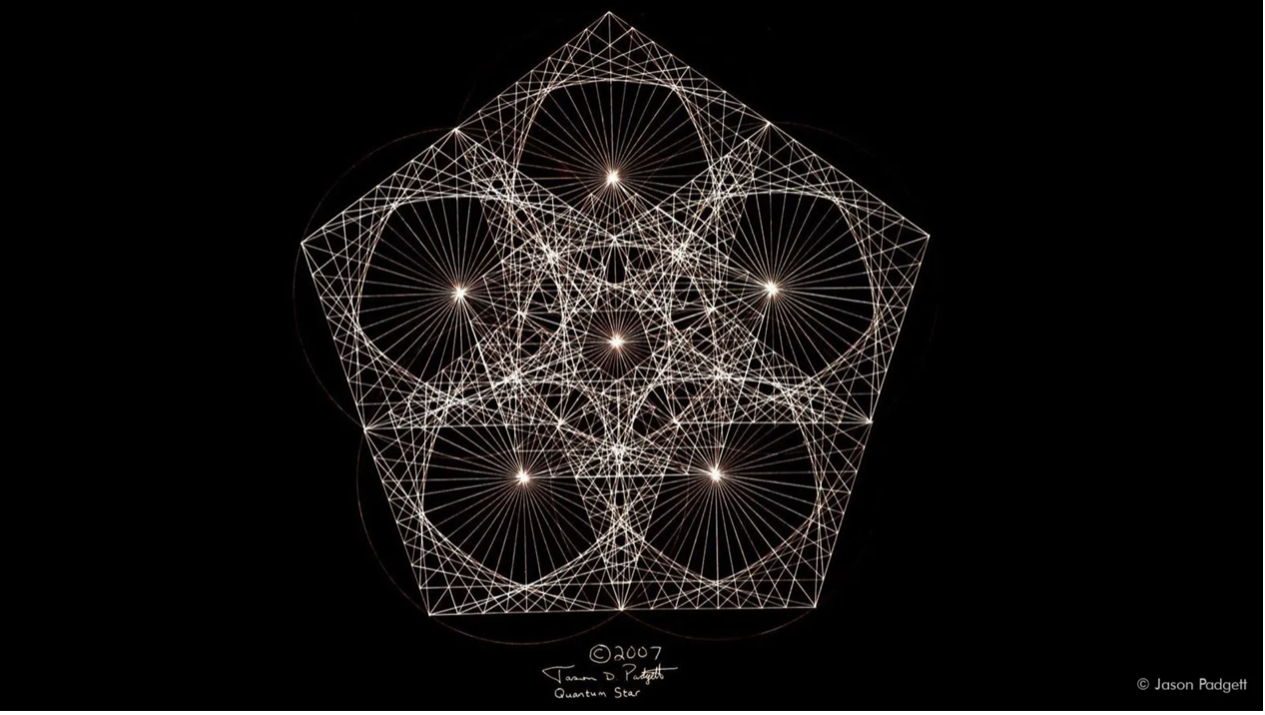Figure 3: Padgett's fractal sketches, Jason Padgett, 2007

Padgett was later diagnosed as suffering from 'Savant Syndrome'; a rare condition which can be a common side effect of trauma (Treffert, 2009). An individual with Savant Syndrome can suddenly develop an ability which they did not previously possess (Incredible Medicine: Dr Weston's Casebook, 2020). Scientists use MRI machines to scan the brain to find 'differences' in a patient with Savant Syndrome.

Professor Berit Brogard, a neuroscientist, carried out research with other such 'Savant Syndrome' patients. One subject had woken up to find he could play the piano despite never having previously learnt that instrument. He too had suffered severe concussion. Following a brain scan, Brogard found his patient had white spots on his brain which were caused by the concussion. The white spots showed damage to the prefrontal cortex; the area of the brain managing rational and logical thinking. To overcome damage, the brain adapts to create new neuron connections and this leads to the development of new skills (Incredible Medicine: Dr Weston's Casebook, 2020).

Padgett was given an MRI to explore his new mathematical superpower. The results revealed that the processing only occurred in the areas of the brain that we do not have conscious access to; the subconscious (Keating, 2020). This supports the idea that his newfound abilities and connection with fractal patterns were in the subconscious area of the brain. Brogard concluded that Padgett now had access to the subconscious areas of his brain as it had made new neuron connections. His ability had always been there; but was inaccessible. In addition, his visual cortex was working simultaneously with the area of the brain responsible for mathematics which explained his sudden interest in a subject he had previously scorned (Keating, 2020).

Afterwards, Padgett saw patterns everywhere and was mesmerised by simple, but usually unnoticeable, actions, such as the ripples of raindrops falling into a puddle (Keating, 2020). "Through Padgett's eyes, the puddle was transformed into complex rippling patterns, overlapping and forming shapes like stars and snowflakes" (Keating, 2020).This supports the idea that fractal recognition is engrained into our subconscious and when brought to the conscious we find it captivating. The transformation in Padgett's brain could be a clue for fractal visual processing in us all and how we have evolved to become such skilled pattern decoders.

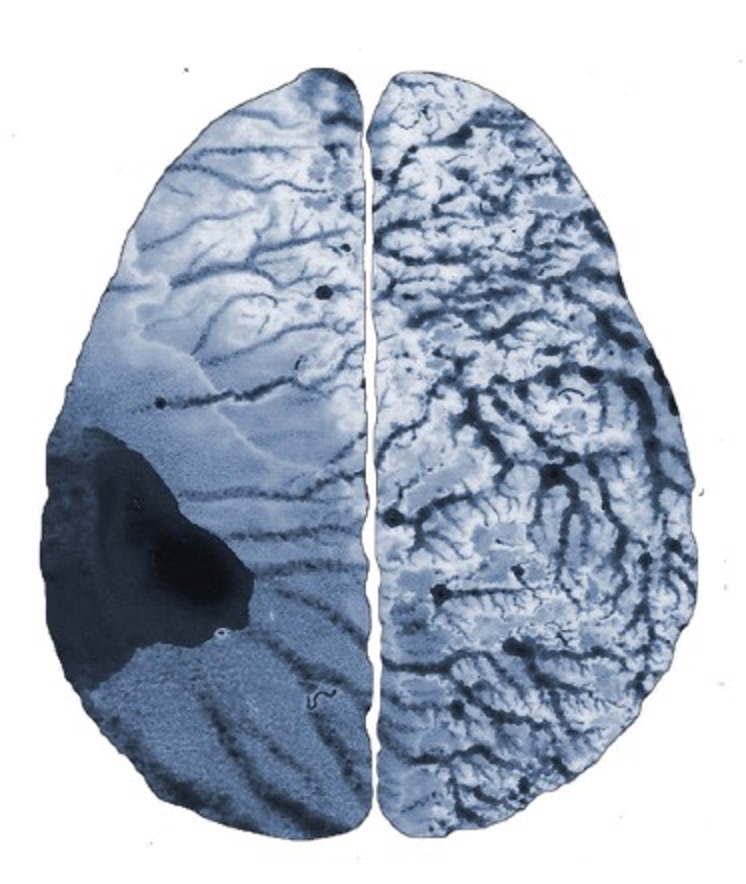
After gaining a greater understanding of Padgett's experience, I explored the role of fractals in the body. Humans are living embodiment of fractals as our blood vessels branch out like root systems and the brain folds within folds of itself. We use these fractal networks; making use of surface area to distribute heat, oxygen and messages around the body (Cepelewicz, 2017). The brain's fractals can be observed through evolution; the more evolved brain has more folds and therefore more fractals (Ventrella, 2012). There is a positive correlation between intelligence and the number of fractals found in the brain (Ray, 2000).

The human visual system is also fractal, which is expressed by the movements of the eye's retina (Robson, 2014).Kang Lee, studied the human ability to recognise patterns. Participants were shown a grey pattern similar to a static television screen and asked to point out what they could see. Despite not being there, participants reported seeing a face 34% of the time; their brain conjuring up a recognisable image. Although we tend to trust what our eyes report, the retina actually sends an inaccurate and confusing image that the brain needs to 'tidy up' (Robson, 2014). This process is called Pareidolia, "a situation in which someone sees a pattern or image of something that does not exist" (Cambridge English Dictionary, n.d.).

Lee concluded that because we see faces from birth, they becomes 'expected' images. This supports the idea that the brain easily recognises familiar patterns and if they are missing, the unconscious mind 'fills in the gap' to produce it. This could, however, be an evolutionary trait, when our ancestors were looking out for faces as a survival technique. We may have inherited this trait, and without realising, constantly seek such patterns (Robson, 2014).

Fractals in the Arts

In this section, I will consider fractals in literature and the creative arts and explore their impact on the human psyche. Fractal dimensions in art are not always obvious. The garden of Kyoto's 15th-century Ryoanji Temple houses a zen meditation garden [fig. 4]. The garden, which consists of just 15 rocks positioned across a rectangular space filled with gravel, has fascinated Western and Eastern travellers for centuries. In 2002, a study was carried out to investigate why the garden was so popular.

Taking a mathematical approach, researchers found the design, which had existed long before the Mandelbrot set and fractal geometry were understood, was fractal in nature (Sarich, 2017). The researchers used computer simulations to rearrange the rocks and found a dramatic decline in the meditative effect. It was noted that despite not knowing about fractals, the designers recognised, on some unconscious level, the calming effect of placing the rocks in that way (Sarich, 2017).

Figure 4: Kyoto's 15th-century Ryoanji Temple houses a zen meditation garden, Shutterstock

Fractal characteristics can be found in a variety of forms including paintings, poetry and music. Studies have shown that pitch fluctuation and rhythm in popular compositions by Bach and Beethoven have a fractal nature (Next Observer, 2019). Taylor argues that music can be fractal as it emerges from and returns to silence (Boon, Casti and Taylor, 2021). The brain's response to music has been verified by taking EEG measurements (Taylor, 2021). Taylor found that mid-fractals produce a strong alpha brain wave response which corresponds to a wakefully relaxed state as well as a strong beta-wave brain which indicates a high ability to concentrate (Boon, Casti and Taylor, 2021).

Taylor explored the impact of mid-range fractals in different art forms on brain activity. He used functional magnetic resonance imaging (fMRI) techniques to study the areas of the brain used for visual processing and spatial memory to show the response of the parahippocampal region, ventrolateral temporal cortex, and dorsolateral parietal cortex. These areas of the brain are responsible for visual processing and spatial memory, as well as regulating emotions; including an emotional response to music (Pierre Boon, Casti and P. Taylor, 2021).

In February 2016, a study carried out on classical books found evidence of a mathematical structure (Drożdżad et al., 2016). After analysing hundreds of texts, in different languages, they found the variation of sentence length obeyed a fractal pattern. All had a similar sentence length and regardless of how expressive they were, showed evidence of a fractal construction. Complex fractal patterns were particularly found in the sentences in James Joyce's, Finnegan's Wake. Much like Jackson Pollock's artwork, which has been described as chaotic, Finnegan's Wake has been described as a "masterpiece of unreadable nonsense" (Alison Flood,2016).

Unlike the chaos and uncertainty of literature, works of art and music can make sense even if we don't quite understand them. That may be why the creations of Pollock, Beethoven and Joyce are so popular. Could they unconsciously access a part of their brain to create something that people would naturally be drawn to? Their works are masterpieces, and have given an insight into the world of fractals; where mathematics and art become one. Hany Farid, a computer scientist, states that "there is an art to mathematics and a mathematics to art" (Rehmeyer, 2007).

Figure 5: Jackson Pollock painting, Summer 1950, Hans Namuth

Jackson Pollock founded the Abstract Expressionism movement. His unique painting style was controversial but pushed modern art forward (Jackson Pollock 1912–1956 | Tate, n.d.). Pollock was the first artist to put fractal theory directly onto a canvas. Despite being seemingly abstract, buried under the splatters and flicks is an underlying level of mathematical structure. His paintings have a deeper meaning to them, a delicate sense of something that looks very messy and chaotic but actually has a very structured code and an order behind it (Lapidus and Doughty, 2005).

Figure 6: Jackson Pollock, 1952, Convergence

Pollack's paintings are gripping and are considered conceptual masterpieces. However, they seem to have captured the wildness of the natural world; no one has been able to pinpoint exactly why his work is so appealing (The Code, 2011). It is possible that the key to Pollock's success lies in the fractal content of his work and the impact that this has on the audiences' subconscious by connecting with something engrained deeply within. Many artists have tried to replicate his work, either through forgery or as an ode to him, however, no one had been able to quite replicate it (The Code, 2011), until Richard Taylor, who had a unique approach to understanding Pollock's work. Taylor built a machine to mimic Pollock's erratic painting style, which he named the 'Pollockieser' [fig. 7].

Figure 7: Still from 'the code' documentary of Richard Taylors 'Pollockiser', 2011

The Pollockieser was designed to replicate the movements of Pollock's hand using a kick pendulum device which, unlike a regular pendulum, which is very regular in its movements, produces a very different type of movement known as "chaotic motion" (The Code, 2011). Pollock's paintings were full of fractal properties and he was able to replicate the same level of fractal complexity at different scales throughout his paintings. When zooming away from the painting [fig. 8, 9, 10, 11], the same patterns appear again and again. All the patterns in his paintings were replicas of each other; regardless of size (The Code, 2011). Taylor's device was successful enough to mimic this particular aspect of Pollock's paintings so that the painting appears the same no matter how closely you look.

Figure 8: Screenshot from documentary the code of Jackson pollocks paintings closely zoomed in, Jackson Pollock

Figure 9: Screenshot from documentary the code of Jackson pollocks paintings slightly zoomed out, Jackson Pollock

Figure 10: Screenshot from documentary the code of Jackson pollocks paintings further zoomed out, Jackson Pollock

Figure 11: Screenshot from documentary the code of Jackson pollocks paintings fully zoomed out, Jackson Pollock

Pollock appeared to be unaware of the complexity in his pieces. When interviewed about his work he states "When I am in my painting, I'm not aware of what I'm doing. It is only after a sort of 'get acquainted' period that I see what I have been about" (Wright and Pollock, n.d.). Although we cannot be sure of his true intentions, Pollock's work has changed and shaped the modern art world (Lapidus and Doughty, 2005). This leads me to wonder whether the use of fractals in Pollock's work could have been unconscious.

The complexity of Pollock's work can be measured by analysing the fractal dimensions. The "Fractal dimension is a measure of how 'complicated' a self-similar figure is; measuring how many 'points' lie in a given set". A line is one dimensional while a plane is two dimensional (Devaney, 1995). Fractal dimensions are calculated by a mathematical equation:

(Fractal Dimension | Mathematics for the Liberal Arts, n.d.)

The calculation of this equation will always give the range between 1 and 2. The more complex the fractal, the closer its dimension is to 2. When Taylor analysed Pollock's paintings in search of fractals, he discovered that the earlier paintings had a lower fractal dimension and as Pollock refined his painting process, they became more complex (Fractals | Encyclopedia.com, 2020). This supports the idea that Pollock was drawn to the fractals that he had created and whether aware or not, he was mesmerised by the swirls of paint before him and carried this on as he developed as an artist.

Pollock's painting style developed organically. Having trouble finishing a painting on an easel, he transferred the painting onto the floor and started experimenting with dripping and flicking paints onto the canvas; stating that he felt "nearer and more a part of the painting" (Pollock, 1987). Pollock mostly used paint brushes and sticks but never physically touched the canvas; waving the implement to flick paint off and onto the canvas.This painting and pouring technique was driven by a need to be more expressive as he looked for newer ways to modernise the art world in a way that suited him and his work; combining his artistic interests in cubism, surrealism and expressionism through increased physical gesture(The Code, 2011). Taylor (2020) states that Pollock's 'fractal detectors' were spurred into action when he saw the patterns that were created by his pouring technique and despite not understanding that the patterns were fractal, Pollock was guided by aesthetics to refine his technique.

Although it is not proven that Pollock was unaware of what he was creating, we can be sure that the paintings came from within his subconscious. When interviewing Pollock, William Wright asked him, if it was true an artist paints from the unconscious and the canvas acts as bridge between the unconscious mind and the viewer. Pollock stated that the unconscious plays an important role when looking at paintings(Wright and Pollock, n.d.).Therefore, indicating his work was based on aesthetics rather than thoroughly thought-out mark-making.

When Pollock's work was first shown to the public, it caused great controversy as his paintings were not what was expected by the art world. However, the abstract flicks, splatters and shapes charmed the audience as their fractal detectors was activated. The public did not know what to think of the work, as it was not seen as 'proper art'; however, as their brains began to recognise the fractal elements, they were inexplicably drawn to his pieces and were captivated. This remains true today as people are in awe of such large, complex but also simple looking pieces of art. The audience often describes a feeling or 'resonance' when Pollock's work is exhibited which results from a shared appreciation of fractals (Taylor, 2020).

One theory is that Pollock's pieces are so engaging because there is an interaction between the painting and the audience. Ruebin Kadish, a friend of Pollock, stated that when viewing a Pollock, there is less emphasis on what is 'seen' and more emphasis on what is 'happening to you' and its impact on the subconscious (Taylor, 2006). Taylor did a series of experiments where he replicated Pollock's work using the Pollockieser. He showed the pieces to a series of participants that looked at both fractal and non-fractal images. His findings were that 95% of the participants preferred the fractal to the non-fractal patterns. This provides some evidence that an inherent appreciation for fractal patterns could explain Pollock's success (Taylor, 2006).

A study was carried out in 2000 using visual perception experiments to explore how the human brain reacts to fractals. The investigation was conducted using eye tracking software at the same time as tracking brain activity. Machines were programmed to generate fractal patterns by building layers of paint to create different levels of complexity. Participants were shown images based on fractals found in Nature, Pollock's fractal paintings and computer-generated fractals. The results indicate that regardless of how the fractals were created, the brain has a similar reaction. There was a universal preference for what are called 'mid complexity' fractals (Taylor and Spehar, 2018).

When analysed, it was found that Pollock's multi-layer technique had resulted in mid-complex fractals. When considering Taylor's findings that participants preferred mid-complex fractals to any other type, this could explain his appeal (Taylor, Spehar, Van Donkelaar and Hagerhall, 2011). This also raises a crucial question about how to harness mid- complex fractals to create other visuals that people are drawn to (Taylor, Spehar, Van Donkelaar and Hagerhall, 2011).

Nature's aesthetic is very powerful and can have a positive impact on the human psyche. In the 1980's architects found that patients who had just received surgery recovered faster if given a room with a window (Ulrich, 1984). Later studies have shown that even photographs of Nature can have a positive effect on the automatic nervous system and affect how people respond to stress (Taylor, 2017). Taylor then set out to understand whether this was related to fractals.

People can efficiently process fractals. This occurs at many stages of the visual system, for example the way our eyes move is related to an area of the brain which is activated when looking at an object or view (Taylor, 2017). Whilst showing participants, computer generated fractals, Taylor used an EEG to record their brain's activity as well as 'skin conductance techniques' to record their stress level. After being shown fractal images, participants had a stress reduction of 60%, supporting the theory that our brains are subconsciously drawn to fractals and offering an explanation about why we like them (Taylor, 2017).

According to Taylor, the fractal rich environment that we surround ourselves with means we don't just enjoy looking at fractals but have a need to look at them (Cepelewicz, 2017). As fractals are so prevalent in nature, we can easily study and consider their complexity. The most common fractal dimensions in Nature, fall between 1.3 and 1.5; low and moderate range (Barlow, 2020).

Taylor explored the preferred range of the fractal complexity scale. He used eye tracking software to precisely measure the movements of the participants' eyes whilst looking at a fractal image. The results indicate that the pupil moves in search patterns mimicking a fractal; first scanning large elements and then making smaller but exactly the same movements as when scanning the larger element. This fractal movement when measured on the complexity scale, falls in the mid-range; just like in Nature. Our brains recognise an affiliation and relationship with the natural world which could explain why we find Nature's fractals so compelling (Cepelewicz, 2017).

Complexity and Contradictions

In this section I will consider the complexity of fractals found in Pollock's paintings and how Taylor's fractal analysis has been used to indicate whether a painting is a genuine 'Pollock'. In 2002/2003 Alex Matter found 32 paintings in his parents' storage unit wrapped in brown paper with indications that they were by Pollock, a family friend. As a 'Pollock' had recently sold for $140 million, Matter was keen to have their authenticity proven. Experts were called including forensic scientists, art experts and Taylor. Fractal analysis was used alongside other scientific and objective tests to determine authenticity. Although stating that his findings should be considered alongside other results, Taylor found that none of the artwork shared the fractal characteristics of Pollock's other paintings (Rehmeyer, 2007).

Katherine Brown, a theoretical physicist, challenged whether Taylor's method could be used to prove whether a painting was created by Pollock. In her article 'Nature (2006)', Brown discredits the theory that Pollock's work was fractal at all. She stated that there are several issues which need consideration before fractal analysis can be used to authenticate paintings; including the small box counting technique Taylor used(Jones-Smith and Mathur, 2006).

Brown created sketches of hand drawn stars using the paintbrush tool in Adobe Photoshop [fig. 13]. When dragging the mouse across the canvas, the paintbrush left a mark and while this was not a drip painting, the patterns are human and not computer generated. She used Taylor's methods to calculate the fractals in Pollock's painting for her own 'childlike drawing' and found that her simple drawing had the same fractal complexity as Pollock's paintings (Jones-Smith and Mathur, 2006). Brown concluded that if fractal complexity was the only factor to be considered, then Pollock's paintings would become trivialised, as comparing them with her basic squiggles had shown them to be on a par. Brown uses this as an argument for stating that Pollock's work should not be considered fractal. Whilst I understand Brown's reasoning, it could be argued that the shapes she drew are unintentionally fractal and supports the theory that her unconscious mind caused her to draw the shapes in a fractal way.

Figure 12: Star sketch, Brown, 2006

Brown argued that the range of fractals, in her picture, were too small to be considered fractal and could easily be replicated and regenerated without the chaotic motion of either freehand drawing or random movements. She argued that as Pollock died in 1956, the only way to reanalyse the way he painted is to watch the few minutes of film we have of him in action (Brown, n.d.). In this footage, Pollock can be heard disputing a claim in Time magazine that his style was chaotic. He was adamant that he could control the paint, that his creations were "no accident" and were ``no chaos, damn it!'' (Pollock, n.d.). Brown believes that Pollock's conviction that he was in control,should be taken into consideration when investigating the mathematical element and level of accuracy in his work (Brown, n.d.).

Brown and her colleagues question the reliability of Taylor's theory. They analysed Pollock's paintings using Taylor's method. Their results indicated that two thirds of Pollock's paintings failed to satisfy the criteria. They suggested Taylor had not published all his methodology and that his sample was too small. They criticised him for only analysing 17 drip paintings when Pollock is known to have produced at least 180. Brown's collaborator, Harsh Mathur, stated that either Taylor was wrong, or Brown's drawings were worth $40 million (Kennedy, 2006).

As part of my research, I contacted Brown to ask about her findings [Appendix 2]. She claims that many images contain identical 'fractal' characteristics so, if Pollock's paintings deserve to be called fractal, so do many others. She includes trivial scribbles that in her opinion have no business being labelled fractal. She believes the more prudent thing to do is not to call Pollock's paintings or the trivial images fractal (Brown, 2021). Brown believes that if fractals are engrained in our subconscious, then it is because, by the very broad definition that people use, they are ever-present to the point of being mundane, and there isn't anything special about them. She disagrees that fractals are engrained into our subconscious and says that Pollock's success had nothing to do with fractals and everything to do with "the state of the world at that time politically and culturally (Brown, 2021).

Taylor responded to Brown's 'Nature' article; declaring that it "would discredit half the published investigations of fractals" (Kennedy, 2006). He claimed that fractal description was physically reasonable because Pollock's method involved a motion dominated process at a large length scale and a paint dominated process at a small scale. He stated that physical responses including motion can be fractal as can falling liquids (Taylor, Micolich† and Jonas, 2006). In response to the criticism of the sample size, Taylor has stated that he is continuing with his research and adding to his sample size (Taylor, 2017).

Mandelbrot, the 'father of fractals' joined the debate, stating that he had extraordinary experience of these structures and believed that Pollock's work is fractal" (Rehmeyer, 2007). Brown and Mathur countered, pointing out that everything would look fractal if you only consider a small range (Rehmeyer, 2007). Brown continues to hold this belief and reiterated this in her email (Appendix 2).

Farid,, a computer scientist used digital forensics to assess and authenticate Mutter's artwork. He commented that regardless of the argument about the fractal nature of Pollock's work, he agreed with Taylor's findings that Mutter's paintings were unlikely to be 'Pollocks'. In addition, the group of experts from Harvard carried out paint analysis and concluded that some paints used would not have been available at the time (Rehmeyer, 2007). Although Brown's findings may show that fractal range analysis is not robust enough to authenticate Pollock's work, I do not believe their argument that his work does not contain fractals.

Conclusion

To conclude, the research I have carried out has developed my understanding of fractals as an infinitely repeating pattern and I now strongly believe that not only are we attracted to fractals but that they are ingrained into our subconscious. Having considered both sides of the argument, I believe I have made an informed decision regarding this theory. We are surrounded with fractals from almost the moment we are born, and our brains are constantly absorbing patterns as well as seeking them out even whilst we are unaware of doing so.

It is not easy to explain the concept of a fractal, yet Pollock's drip paintings make it possible to recognise them. This is true even without knowing the mathematics behind them. Once fractals are understood to be a part of the conscious mind, they appear everywhere, and this is something I have been able to witness first-hand. Since discovering fractals, I have come to realise that almost everything in existence is somehow related to fractal geometry. I see them everywhere and am now keenly aware of them, and of how much I search for them.

Despite Brown's contradictory research regarding fractals, stating they could be seen as mundane and therefore not ingrained into our subconscious, research carried out by psychologists, physicists and artists suggest that fractals are ingrained into our minds. The case study of Padgett indicated that fractals exist within the subconscious mind and scientific and medical investigations, including MRI scans, showing that the areas of the brain controlling unconscious thought were stimulated when Padgett was shown images.

Evolution is given as a possible explanation for why humans are pattern seekers as seeing patterns can aid survival. We see evidence of face recognition patterns from a study, where participants reported seeing a face in grey static patterns even though they were not there because they were trying to make sense of what they were seeing. This supports the theory that when we are surrounded by something, we unconsciously search for it.

Fractals can be found in a variety of places including nature, the human body, music, art and activity. These are easily found in the natural environment and have a well-documented, positive and comforting effect; helping to heal the sick, calm the agitated and awaken the soul. The complexity of a fractal can be calculated, and studies have shown that humans have a collective preference for mid-range fractals. The very action of searching for a fractal is fractal in nature and this also has a mid-range dimension. Mid-range fractals have also been found in artwork and can be used like a fingerprint to aid identification of the artist. They can also be found in musical compositions and have been shown to aid concentration and relaxation. These findings have made me want to further investigate whether mid-range fractals are the reason we are drawn to particular creative works.

Bibliography

Ball, P., 2016. Patterns In Nature. Chicago: The University of Chicago Press.

Barlow, J., 2020. Like Adults, Children By Age 3 Prefer Seeing Fractal Patterns: Study Concludes That Preference For Common Natural Patterns May Develop Early In Life. [online] ScienceDaily. Available at: https://www.sciencedaily.com/releases/2020/12/201211135507.htm#:~:text=%22We%20found%20that%20people%20prefer,process%20images%2C%22%20Robles%20said. [Accessed 12 January 2021].

Brown, K., 2021. Jackson Pollocks Fractal Research. [email].

Brown, K., n.d. Kate Brown - Fractals And Jackson Pollock - Hamilton College. [online] People.hamilton.edu. Available at: https://people.hamilton.edu/kbrown/fractals-and-jackson-pollock [Accessed 15 January 2021].

Cepelewicz, J., 2017. Is Consciousness Fractal?. [online] Nautilus. Available at: http://nautil.us/issue/47/consciousness/is-consciousness-fractal [Accessed 11 January 2021].

Courses.lumenlearning.com. n.d. Fractal Dimension | Mathematics For The Liberal Arts. [online] Available at: https://courses.lumenlearning.com/waymakermath4libarts/chapter/fractal-dimension/ [Accessed 11 January 2021].

Da Vinci, L., 2012. The Notebooks Of Leonardo Da Vinci, Vol. 1. 1st ed. Newburyport: Dover Publications, p.206.

Devaney, R., 1995. Fractal Dimension. [online] Math.bu.edu. Available at: http://math.bu.edu/DYSYS/chaos-game/node6.html [Accessed 11 January 2021].

Dictionary.cambridge.org. n.d. PAREIDOLIA | Meaning In The Cambridge English Dictionary. [online] Available at: https://dictionary.cambridge.org/dictionary/english/pareidolia [Accessed 12 January 2021].

Drożdżad, S., Oświȩcimkaa, P., Kuliga, A., Kwapieńa, J., Bazarnikb, K., Grabska-Gradzińskac, I., Rybickib, J. and Stanuszekd, M., 2016. Quantifying Origin And Character Of Long-Range Correlations In Narrative Texts.

Encyclopedia.com. 2020. Fractals | Encyclopedia.Com. [online] Available at: https://www.encyclopedia.com/education/news-wires-white-papers-and-books/fractals [Accessed 11 January 2021].

Fractals and Jackson Pollock. 2011. [film] Directed by A. Matt. Independent.

Freud, S., Strachey, J., Freud, A., Strachey, A. and Tyson, A., 2001. The Standard Edition of The Complete Psychological Works Of Sigmund Freud. London: Vintage, p.57.

Gordon, N., Rood, W. and Edney, R., 2009. Fractals. Lanham, Md: Totem Books.

Harmon, J., 2016. Patterns: The Need For Order. [online] Psych Central. Available at: https://psychcentral.com/lib/patterns-the-need-for-order [Accessed 16 November 2020].

Hunting the Hidden Dimension. 2008. [DVD] Directed by M. Schwarz and B. Jersey. NOVA.

Incredible Medicine: Dr Weston's Casebook. 2020. [video] England: BBC 2.

Jackson Pollock. 1987. [film] Directed by K. Evans. USA.

Jones-Smith, K. and Mathur, H., 2006. Revisiting Pollock'S Drip Paintings Arising From: R. P. Taylor, A. P. Micolich And D. Jonas Nature 399, 422 (1999). [online] pp.1-2. Available at: https://doi.org/10.1038/nature05398 [Accessed 14 January 2021].

Jones-Smith, K., 2006. Untitled 5. [image] Available at: https://doi.org/10.1038/nature05398 [Accessed 17 January 2021].

Keating, S., 2020. The Violent Attack That Turned A Man Into A Maths Genius. [online] BBC.com. Available at: https://www.bbc.com/future/article/20190411-the-violent-attack-that-turned-a-man-into-a-maths-genius [Accessed 11 January 2021].

Kennedy, R., 2006. The Case of Pollock's Fractals Focuses on Physics. New York Times, [online] Available at: https://www.nytimes.com/2006/12/02/books/02frac.html [Accessed 15 January 2021].

Lapidus, F. and Doughty, B., 2005. Jackson Pollock Invented A New Kind Of Painting That Changed The Way People Looked At Art. [online] VOA. Available at: https://learningenglish.voanews.com/a/a-23-2005-10-15-voa2-83123777/123976.html [Accessed 10 January 2021].

Lexico Dictionaries | English. n.d. Fractal | Definition Of Fractal By Oxford Dictionary On Lexico.Com Also Meaning Of Fractal. [online] Available at: https://www.lexico.com/definition/fractal [Accessed 10 January 2021].

Lexico Dictionaries | English. n.d. Subconscious | Definition Of Subconscious By Oxford Dictionary On Lexico.Com Also Meaning Of Subconscious. [online] Available at: https://www.lexico.com/definition/subconscious [Accessed 8 January 2021].

Mandelbrot, B., 1983. The Fractal Geometry Of Nature. New York: W.H. Freeman.

Moore, J., n.d. History Of Fractals | Sk33lz Is A Geek. [online] Sk33lz.com. Available at: https://sk33lz.com/create/fractals/history-fractals#:~:text=Fractals%20%2D%20The%20Beginning,replica%20of%20the%20whole%20shape. [Accessed 8 December 2020].

Next Observer, 2019. Is Consciousness Fractal?. [video] Available at: https://www.youtube.com/watch?v=Ig7TwCg4jTI&t=22s [Accessed 7 December 2020].

Observer, N., 2020. Is Consciousness Fractal? – The Engineering Of Conscious Experience. [online] Theengineeringofconsciousexperience.com. Available at: https://theengineeringofconsciousexperience.com/is-consciousness-fractal/ [Accessed 4 January 2021].

Overweening Generalist, 2012. Drippy Jackson Pollock Theories: Art and Mathematics!. Available at: http://overweeninggeneralist.blogspot.com/2012/11/drippy-jackson-pollock-theories-art-and.html [Accessed 14 January 2021].

Padgett, J., 2020. The Violent Attack That Turned A Man Into A Maths Genius. [online] Bbc.com. Available at: https://www.bbc.com/future/article/20190411-the-violent-attack-that-turned-a-man-into-a-maths-genius [Accessed 11 January 2021].

Peitgen. and Reizakis., 1986. Beauty Of Fractals. [S.l.]: Springer Berlin Heidelberg.

Pierre Boon, J., Casti, J. and P. Taylor, R., 2021. Artistic Forms And Complexity. [online] Richard Taylor. Available at: https://cpb-us-e1.wpmucdn.com/blogs.uoregon.edu/dist/e/12535/files/2015/12/FractalMusicAndArt-1mxlbkx.pdf [Accessed 16 January 2021].

Pollock, J., n.d. [Video] https://www.sfmoma.org/watch/jackson-pollock-paintings-have-a-life-of-their-own/, San Francisco.

Ray, C., 2000. Q & A; Brain Folds (Published 2000). [online] Nytimes.com. Available at: https://www.nytimes.com/2000/10/31/science/q-a-brain-folds.html [Accessed 11 January 2021].

Rehmeyer, J., 2007. Fractal Or Fake? - Novel Art-Authentication Method Is Challenged. Science and Technology. [online] Sott.net. Available at: https://www.sott.net/article/127532-Fractal-or-Fake-Novel-art-authentication-method-is-challenged [Accessed 15 January 2021].

Robson, D., 2014. Neuroscience: Why Do We See Faces In Everyday Objects?. [online] Bbc.com. Available at: https://www.bbc.com/future/article/20140730-why-do-we-see-faces-in-objects [Accessed 12 January 2021].

Sarich, C., 2017. This 15Th Century Zen Rock Garden Used Fractal Geometry. [online] The Mind Unleashed. Available at: https://themindunleashed.com/2017/11/this-15th-century-zen-rock-garden-used-fractal-geometry.html [Accessed 16 January 2021].

Shermer, M., 2003. How We Believe. 2nd ed. New York: H. Holt, p.59.

Shermer, M., 2008. Scientific American. [online] Patternicity: Finding Meaningful Patterns in Meaningless Noise. Available at: https://www.scientificamerican.com/article/patternicity-finding-meaningful-patterns/ [Accessed 6 January 2021].

Shukla, A., 2020. Why Did Humans Evolve Pattern Recognition Abilities?. [online] Cognition Today. Available at: https://cognitiontoday.com/why-did-humans-evolve-pattern-recognition-abilities/#:~:text=Assigning%20patterns%20itself%20is%20a%20cognitive%20skill%20that%20survived%20evolutionary%20hurdles.&text=In%20short%2C%20pattern%20recognition%20was,efficient [Accessed 17 January 2021].

Tate. n.d. Jackson Pollock 1912–1956 | Tate. [online] Available at: https://www.tate.org.uk/art/artists/jackson-pollock-1785 [Accessed 26 November 2020].

Taylor, R. and Spehar, B., 2018. FRACTAL GEOMETRY OF THE BRAIN. [Place of publication not identified]: SPRINGER, pp.485-496.

Taylor, R., 2006. Personal Reflections On Jackson Pollock's Fractal Paintings. [online] Scielo. Available at: https://www.scielo.br/scielo.php?script=sci_arttext&pid=S0104-59702006000500007 [Accessed 12 December 2020].

Taylor, R., 2017. Fractal Patterns In Nature And Art Are Aesthetically Pleasing And Stress-Reducing. [online] The Conversation. Available at: https://theconversation.com/fractal-patterns-in-nature-and-art-are-aesthetically-pleasing-and-stress-reducing-73255 [Accessed 12 January 2021].

Taylor, R., 2017. The facts about Pollock's fractals. [Blog] Richard Taylor, Available at: https://blogs.uoregon.edu/richardtaylor/2017/01/04/the-facts-about-pollocks-fractals/ [Accessed 9 November 2020].

Taylor, R., 2021. The Potential Of Biophilic Fractal Designs To Promote Health And Performance: A Review Of Experiments And Applications. Sustainability. [online] MDPI, p.6. Available at: https://doi.org/10.3390/su13020823 [Accessed 16 January 2021].

Taylor, R., Micolich†, A. and Jonas, D., 2006. Taylor Et Al. Reply. Fractal Analysis. [online] Nature, p.2. Available at: https://doi.org/10.1038/nature05398 [Accessed 15 January 2021].

Taylor, R., Spehar, B., Van Donkelaar, P. and Hagerhall, C., 2011. Perceptual and Physiological Responses to Jackson Pollock's Fractals. Frontiers in Human Neuroscience, 5.

Taylor, R., n.d. Fractals Found In Pollocks Paintings. [email].

The Code. 2011. [film] Directed by M. Lachmann. England: BBC2.

The Guardian, 2016. Scientists find evidence of mathematical structures in classic books. [online] Available at: https://www.theguardian.com/books/2016/jan/27/scientists-reveal-multifractal-structure-of-finnegans-wake-james-joyce [Accessed 16 January 2021].

Treffert, D., 2009. Savant Syndrome - An Overview | Sciencedirect Topics. [online] Sciencedirect.com. Available at: https://www.sciencedirect.com/topics/neuroscience/savant-syndrome [Accessed 11 January 2021].

Ulrich, R., 1984. View Through A Window May Influence Recovery From Surgery | The Center For Health Design. [online] Healthdesign.org. Available at: https://www.healthdesign.org/chd/knowledge-repository/view-through-window-may-influence-recovery-surgery [Accessed 12 January 2021].

Ventrella, J., 2012. Brainfilling Curves. [Place of publication not identified]: Eyebrain Books, p.14.

Weiss, B., 2017. [video] Available at: https://www.ted.com/talks/ben_weiss_fractals_a_world_in_a_grain_of_sand [Accessed 26 November 2020].

Williams, f., 2017. Why Fractals Are So Soothing. [online] The Atlantic. Available at: https://www.theatlantic.com/science/archive/2017/01/why-fractals-are-so-soothing/514520/ [Accessed 12 January 2021].

Wright, W. and Pollock, J., n.d. Jackson Pollock: An Interview. [online] Interview Transcript. Available at: http://homepages.neiu.edu/~wbsieger/Art201/201Read/201-Pollock.pdf [Accessed 10 December 2020].

Appendices

Appendix 1

Fractals found in Pollocks paintings

Rachel Garvey

Hi, I am currently a final year arts student at University in London and am writing my dissertation about patterns in nature (fractal patterns) and have come across your works surrounding Jackson Pollock. Do you think at the time of making his paintings he was aware of the fractal like images he was painting? And do you think that is why his paintings were successful? Are we born with a subconscious of recognising the patterns around us and although not aware at the time we can recognising fractal images?

Any of your thoughts and opinions would be much appreciated, I am also attempting to create. my own drawing machine that will create fractal like patterns

Thank you

Rachel Garvey

Richard Taylor

Hi Rachel

Thanks for contacting me.

May Pollock research triggered a set of psychology experiments aimed at the aesthetics of his fractals - but it quickly broadened to what we now call 'fractal fluency.' Because our visual systems have evolved surrounded by nature's fractals, our vision has become fluent in the visual language of fractals. More specifically, our ours are excellent fractal detectors when then they do detect fractals this induces a profound aesthetic effect.

Pollock developed the pouring technique driven by a need to be more expressive (he wanted to combine his artistic interests in cubism, surrealism and expressionism through increased physical gesture). However, once he saw the fractals that were naturally created by his pouring technique this called his fractal detectors into action. I'm confident that he then refined the technique guided by this aesthetic (even though, consciously, he didn't realize that the patterns were fractal).

All of our eyes are fractal detectors and so that feeling or 'resonance' that people often describe when looking at pollock's work is a result of this shared appreciation of fractals.

There are some general articles that hopefully explain this in a non technical manner: https://blogs.uoregon.edu/richardtaylor/2016/02/03/human-physiological-responses-to-fractals-in-nature-and-art/

The 6th one down the list, in the journal of Biourbanism is a good one!

Take are, Richard

Appendix 2

Jackson Pollocks Fractal Research

Rachel Garvey

Hi Kate, Hope you are well

I am a third-year graphic design student at the University of the Arts London, I am currently writing my dissertation on fractals and whether they are engrained into us subconsciously. I have come across your research of his work not being fractal and want to ask you if this is still something you believe?

I also would like to ask what your opinions on fractals being ingrained into us are and whether or not you think this to be true.

If not why do you believe Pollock's work became so successful in a time that was not used to any works similar to his?

I really appreciate any response you have to these questions as they would really help my own research, and I appreciate any time you have taken to read this email.

Thank you

Rachel Garvey

Katherine (Kate) Brown

Hi Rachel,

Thanks for contacting me. I have a great deal to say about Pollock and fractals so I'm happy to elaborate on any of this or provide proof of these claims if you'd like. I strongly disagree with the idea that fractals are engrained into us subconsciously. To answer your questions directly

I have come across your research of his work not being fractal and want to ask you if this is still something you believe?

Yes, correct: Pollock's work cannot be meaningfully characterized as fractal. We have shown unambiguously that the purportedly fractal characteristics present in Pollock's work are also present in crude sketches and trivial images. In fact these 'fractal' characteristics are not robust properties of an image in the sense that they can be manipulated or produced at will. Many other images contain identical 'fractal' characteristics; so, if Pollock's paintings deserve to be called fractal, many other images also deserve to be called fractal. That includes trivial scribbles that in my opinion have no business being labelled fractal. Thus, I think the more prudent thing to do is NOT call Pollock's paintings or the trivial images fractal.

I would not characterize this as my 'belief' but rather something we have shown rigorously, beyond any reasonable scientific doubt. As a scientist, I accept logically sound hypotheses that are supported by data as facts rather than beliefs. There is a long history of scientists being overzealous and excessive in their labelling of real-world systems as fractal, even according to the father of fractals himself, Mandelbrot. Some scientists persist in labelling many things as fractal (including Pollock's paintings and artwork other than Pollock's) even in the face of evidence to the contrary. But I believe that is irresponsible and scientifically imprudent.

I think people are drawn to the idea that fractals are present in artwork, but that is different from there actually being meaningful fractal content in artwork. A responsible scientist is guided by data and presents their data transparently. We have presented copious evidence that Pollock's paintings cannot be meaningfully characterized as fractal, but people will believe what they want to believe.

If not why do you believe Pollock's work became so successful in a time that was not used to any works similar to his?

The reception of Pollock's work is not my area of expertise, I defer to art historians here, but I don't think the success of his work has anything to do with fractals. I note that fractals were not invented/understood mathematically for about 20 years after Pollock died. And, many people were extremely critical of his work when he first started drip painting, i.e. it was not universally well-received. In fact his work was arguably quite controversial. I also note that he was influenced heavily by other artists, some of whom were in fact producing drip paintings and work that looks similar to what we now associate as Pollock's signature style.

I think the success of his work has to do with many things... the state of the world at that time politically, culturally; the state of the art world at that time. But it has absolutely nothing to do with fractals.

Images that are boring and trivial and that don't excite people or calm people or even interest people have exactly the same 'fractal' content as his paintings. If you use a very broad definition of fractal (as I believe most people do), then everything is fractal. To the extent that Jackson Pollock's paintings are fractals, so too are a lot of other images, and thus Pollock was not unique in his ability to create them. If fractals are engrained in our subconscious, then it is because, by the very broad definition that people are inclined to use, they are utterly ubiquitous to the point of being mundane, and there isn't anything special about them.

Please let me know if there is anything I can clarify or back up here. Good luck with your work and thanks for asking me to weigh in.

Sincerely,

Kate